To successfully apply a roulette computer, the player must be able to receive an accurate prediction before the dealer calls no more bets. With the typical roulette computer, because dealers spin the ball at different speeds, you will find that many dealers don’t spin the ball fast enough for the ball to even reach the target speed (especially after you’ve just clocked a slow rotor). This makes the typical roulette computer algorithm impractical in many circumstances, and is particularly frustrating as you may need to wait hours for a suitable dealer to return. It is the same case with visual ballistics methods. Remember that both the simple roulette computer and visual ballistic algorithm involve waiting for the ball to reach a target speed, and then obtaining a prediction. As this can be impractical with different dealers, a computer often needs to be able to predict at any ball speed for application to be practical.
Linear Vs Actual Ball Deceleration Curves
The very first version of my computers were capable of obtaining predictions at anytime in the spin. This is possible only with sophisticated algorithms, unless you sacrifice accuracy with a simplistic solution. To obtain predictions anytime in the spin, rather than targeting a specific ball speed, you cannot simply assume the ball deceleration is linear. Assuming it is linear is assuming that the ball deceleration will be constant no matter what the ball speed is, and it is a critical mistake.
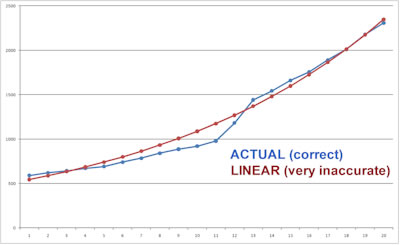
Linear vs polynomial
Shown above are two curves for the same ball timings. This is from a John Huxley Mk7 roulette wheel with Velstone ball track, which is one of the latest roulette wheels. The blue line shows the exact and actual timings with an ivorine ball. The red line shows the deceleration if you incorrectly assumed it to be linear. The red line looks smooth and accurate, but to give you an idea of how inaccurate the linear assumption is, consider that between two dots represents just one ball revolution. The data shows that at some ball speeds, the linear line is approximately between 0 – 2 full revolutions inaccurate.
This means that if you assume the ball deceleration is linear, on some spins you will be accurate enough (target the correct revolution), on some spins you will be 1 revolution off target, and other revolutions you will be about 2 more revolutions off target. This results in very poor or no accuracy, and this is only assuming you are still using a very basic approach where you solely consider rotor position at estimated ball drop time. If the ball deceleration is smoother without the distinct bend which is very common on wheels, then the deviation will be between 0-1 ball revolution at best. This would then be acceptable, but only if you are playing on a wheel with a very strong dominant diamond. However, a deviation of 0-1 revolutions is enormous and unacceptable if you are using any advanced approaches, such as targeting which diamond the ball will hit. That is unless you are predicting which diamond will be hit when the ball is just about to actually hit the diamond, in which case there is no point because you can’t bet that late.
In summary, assuming ball deceleration is linear is a “cheap shortcut”, and is only acceptable if you intend to play only very easily beaten and rare wheels (wheels where the ball barely bounces, and almost always hits the same diamonds). But if you intend to play on modern wheels, you will be unable to achieve significant accuracy.
My Lite, Uber and Hybrid computers all correctly model the actual ball deceleration curve. They do NOT assume the ball deceleration is linear and use a much more complex algorithm. Therefore my computers can obtain predictions anytime in the spin without a significant loss in accuracy. However, only the Uber and Hybrid computers are capable of dynamically adjusting for ball deceleration rate changes.
Misleading Demo Videos
Only two other roulette computers are capable of obtaining predictions anytime in the spin. However, they both incorrectly assume ball deceleration is linear. In particularly, one vendor creates deceptive videos in which he promotes his computer’s ability to obtain predictions anytime in the spin. Specifically he continuously clocks the ball in a recorded spin on dvd, and shows how close each prediction is to each other. Basically the closer the predictions are, the better. This may seem impressive without sufficient knowledge, but in reality he is merely demonstrating:
- How linear the ball’s deceleration is on one particular wheel
- His computer’s ability to target a specific revolution
The second point is most relevant. You may recall how in earlier pages I explained how even a poorly designed computer with inaccurate timings can target when there are 4,5,6 or so revolutions are remaining. And that the timings for the last few revolutions are much the same between different spins. So there are only two possibilities for what his algorithm does: either considers complete revolutions, or partial revolutions.
If he used complete revolutions, predictions will almost always be exactly the same number, with the occasional jump to a different number (because it may occasionally lock onto the wrong revolution). So mostly two particular numbers will be predicted. But if he considers partial revolutions, then it is impossible to apply the algorithm on anything but wheels with very strong dominant diamonds and with minimal scatter. Additionally, as the variation in accuracy on individual spins will range between 0-2 ball revolutions, there is absolutely no chance his assumption of linear ball deceleration can achieve even close to maximum accuracy. To better explain how you can easily replicate this “anytime prediction”, test on a recorded spin and guess when there are about 10 seconds until the ball falls. Then count down each revolution, 9,8,7,6 etc down to 0. If you were correct to within 1 revolution accuracy, congratulations, you have just replicated the “anytime predictions” without a device. Certainly it sounds overly simplistic, and it isn’t any great achievement. But when a computer repeatedly predicts around the same number on each revolution, it appears more impressive despite it being essentially the same thing.
Ultimately his device’s assumptions are an inappropriate and limited shortcut. To keep predicting the same number on the same spin with subsequent clicks, he would only need to continue clicks while the ball speed is linear enough to be accurate to within about 250ms. Again consider that the average clocking error is 50ms. In other words, the incorrect assumption of linear deceleration may be acceptable on a very easily beaten wheel where advanced algorithms are not required. But if a wheel requires advanced algorithms, the loss in accuracy is far too great for the advanced algorithm to be viable. Also importantly, this is assuming the device performs other required functions perfectly.
How Our Computers Model Ball Deceleration
Polynomial Vs Actual
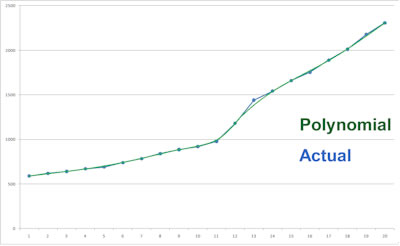
My computers use a combination of advanced polynomials and actual ball timings to accurately model the true ball deceleration. Shown left is an example of a polynomial curve (green) with the actual ball timings (blue). You can clearly see it is far more accurate than linear assumption. The deviation from precise timings is barely noticeable.
These charts can be seen in my roulette computer’s settings. Additionally, the polynomial order value can be changed to accurately deal with any distinct bends in the ball deceleration curve. The much better “curve fit” ensures that a high degree of accuracy is maintained even when the computer user needs to obtain predictions anytime in the spin. With the exception of splines which have some disadvantages, use of high order polynomials is the only accurate method of modelling a relatively complex curve.
Putting it all together
In addition to accurate initial modelling of the deceleration curve, as discussed in previous sections, the ball’s deceleration curve will change. So the computer must learn the ball’s deceleration. This is a complex problem that only my Uber and Hybrid computers solve. Without automatic learning of ball deceleration rate changes, even an accurate initial modelling will eventually become obsolete as the ball deceleration changes.
But assuming everything to this point is done correctly, now the computer user needs to be able to get all timings (clicks) done, receive the prediction, then place bets all before the dealer calls no more bets. With a typical roulette computer, you need to first clock the rotor (one click each time zero passes the diamond to take the rotor timing), then make your clicks for the ball. Some of the problems that need to be overcome are:
- Correct modeling and learning of ball deceleration: (as already discussed)
- Getting ENOUGH clicks in time: this is essential. You can easily get a prediction with 2 ball clicks (1 revolution), but it wont give you enough accuracy. A common problem with basic computers is that when the ball is released, the rotor’s green zero has already passed the reference diamond you use for timings. This means you’d need to wait for the rotor to come all the way back around before you can clock it. This wastes 3-5 seconds. Then after you finally clock the rotor, you can clock the ball but it is often too late as the ball is either too slow, or the prediction is too late to bet.
Our hybrid roulette computer does everything automatically without any “clocking”, so it is inappropriate to compare other devices to it.
